С. І. Доценко. Розподіл витрат в задачі розвозки

On Чер 11, 2021

Вступ. У даній статті розглянута логістична задача справедливого розподілу витрат при доставці вантажів декільком споживачам. На інтуїтивному рівні зрозуміло, що якщо сумарний обсяг замовлень не перевищує вантажопідйомності транспортного засобу, то групі споживачів вигідніше вскладчину оплатити деякий кільцевий маршрут, ніж кожному окремо платити за радіальний. Виявляється, що математичним апаратом такого завдання розподілу витрат може служити кооперативна гра, “надбудована” над задачею комівояжера.

Основні відомості про задачу комівояжера.

Вступ. Задача комівояжера є однією з ключових завдань комбінаторної оптимізації. Вона формулюється так: в графі знайти замкнутий маршрут мінімальної ваги (де під вагою маршруту розуміється сума ваг входять до нього ребер), в який кожна вершина входить в точності один раз.

Щодо постановки завдання комівояжера слід зробити деякі зауваження. У довільному графі (наприклад, в будь-якому дереві) може не існувати замкнутого маршруту, що містить кожну з вершин в точно-сті один раз. Навіть якщо такий маршрут існує, то може існувати маршрут меншої ваги, що проходить через всі вершини принаймні один раз, а через деякі вершини – більше одного разу. Однак в повному графі за умови дотримання нерівності трикутника для будь-якої трійки вершин існує замкнутий маршрут з відвідуванням кожної вершини рівно один раз, для якого не існує іншого замкнутого маршруту з відвідуванням кожної вершини по крайней мере один раз і має меншу вагу.

Як приклад, розглянемо задачу розвезення з відправною точкою в Києві з відвідуванням чотирьох центрів областей, що межують з Київською – Вінниці, Житомира, Чернігова і Черкас.

В якості вихідних даних завдання візьмемо відстані між містами автомагістралями, обчислені за допомогою онлайн-калькулятора відстаней на сайті avtodispetcher.ru. Таблиця відстаней між містами має вигляд:

Таблиця 1.

	К	Чн	Ж	В	Чк
Київ	–	142	140	267	194
Чернігів	142	–	282	408	301
Житомир	140	282	–	127	330
Вінниця	267	408	127	–	354
Черкаси	194	301	330	354	–

Відзначимо, що для даних відстаней між містами для будь-якої трійки міст виконується нерівність трикутника.
Для задачі розвезення по кільцевому маршруту побудуємо еквівалентну кооперативну гру, в якій гравцями є все міста, крім відправного пункту (в даному випадку Києва), а в якості характеристичної функції (коаліції міст) береться найкоротший кільцевий маршрут, що виходить з відправного пункту і проходить через всі міста даної коаліції.

Знайдемо значення характеристичної функції для всіх можливих коаліцій.

Значення функції для одноелементні коаліцій одно подвоєному відстані від Києва до даного міста і тоді
V (Чн) = 284, V (Ж) = 280, V (В) = 534, V (Чк) = 388. (1)

Значення функції для двоелементний коліцій дорівнює сумі трьох доданків – відстаней т Києва до цих міст і відстані між ними, тоді
V (Чн, Ж) = 284, V (Чн, В) = 817, V (Чн, Чк) = 637, V (Ж, В) = 534, V (Ж, Чк) = 664, V (В, Чк ) = 815.

Значення функції для коаліцій з трьох і чотирьох елементів обчислюємо, як оптимальне рішення задачі комівояжера по маршруту, що включає Київ і дані міста. При цьому можна скористуватись онлайн-сервісом на сайті math.semestr.ru.

Даний сервіс дозволяє розв’язувати задачу комівояжера для кількості міст, що не перевищує 14 методом гілок і меж, при цьому генерується докладний протокол покрокового рішення.

Результати обчислень представлені в таблиці 2.

Таблиця 2.

Коалиция	Маршрут	Довжина
(Чн, Ж, В)	К-Чн-В-Ж-К	817
(Чн, Ж, Чк)	К-Чн-Чк-Ж-К	913
(Чн, В, Чк)	К-Чн-Чк-В-К	1064
(Ж,В,Чк)	К-Ж-В-Чк-К	815
(Чн,Ж,В,Чк)	К-Чн-Чк-В-Ж-К	1064

Розглянемо наведену характеристическую функцію W(S), яка для кожної коаліції висловлює “сумарну економію довжини маршруту” і дорівнює сумі довжин радіальних маршрутів мінус довжина найкоротшого кільцевого маршруту, тобто

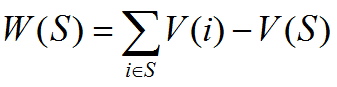
Наприклад, для гранд-коаліції дана величина становить
W (Чн, Ж, У, Чк) = V (Чн) + V (Чк) + V (В) + V (Ж) – V (Чн, Ж, У, Чк) = 422.

Для зручності обчислень замінимо назви міст номерами, наприклад в порядку, відповідному найкоротшому кільцевому маршруту, що включає всі міста, тобто 1-Чернігів, 2-Черкаси, 3-Вінниця, 4-Житомир, тоді значення характеристичної функції має вигляд:
W (1) = W (2) = W (3) = W (4) = 0, W (1,2) = 35, W (1,3) = 1, W (1,4) = 0, W (2,3) = 107, W (2,4) = 4,
W (3,4) = 280, W (1,2,3) = 387, W (1,2,4) = 39, W (1,3,4) = 281, W (2,3,4) = 387, W (1,2,3,4) = 422.

Зауважимо, що для даної характеристичної функції порушується умова сніжної грудки, а отже, умова опуклості. дійсно,
Add (1, (2,3)) = W (1,2,3) -W (2,3) = 280; Add (1, (2,3,4)) = W (1,2,3,4) -W (2,3,4) = 35.

У цьому випадку вектор Шеплі може і не належати ядру.
Для випадку чотирьох гравців 1-я компонента вектора Шеплі може бути обчислена за формулою

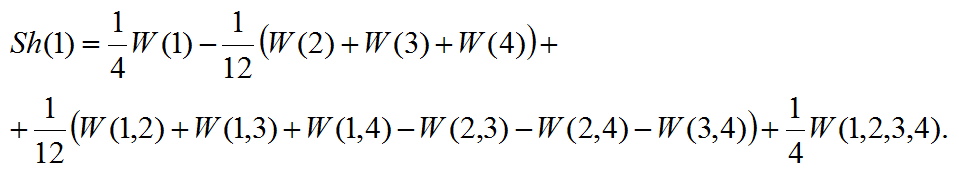
Оскільки характеристичний функція є наведеної і значення функції від одноелементні коаліцій дорівнюють нулю, то формула спрощується:

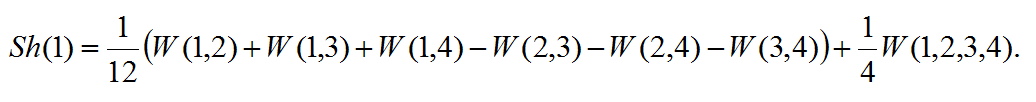
Інші компоненти В.Ш. можуть бути обчислені за формулами, одержуваних з даної циклічної перестановкою аргументів. Таким чином

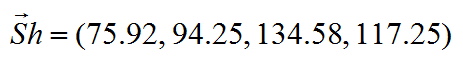
Зауважимо, що в даному випадку В.Ш. не належить ядру. Дійсно, для коаліції {3,4} має місце порушення умови стабільності:
В даному випадку розподіл економії згідно вектора Шеплі представляється неприйнятним. Як альтернативний варіант розподілу можна вибрати
n-ядро або npc-ядро (nucleolus per capita).
Знайдемо n-ядро даної гри. Для цього потрібно буде вирішити ланцюжок завдань лінійного програмування (ЗЛП). Перша ЗЛП ланцюжка зводиться до максимізації мінімальної з переплат по набору всіх можливих коаліцій, за винятком порожній коаліції і гранд-коаліції. Нехай t- шукана величина мінімальної переплати, тоді ЗЛП набуває вигляду:

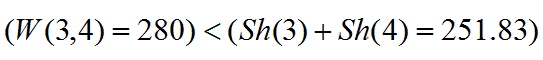
Для даної характеристичної функції перша ЗЛП має вигляд: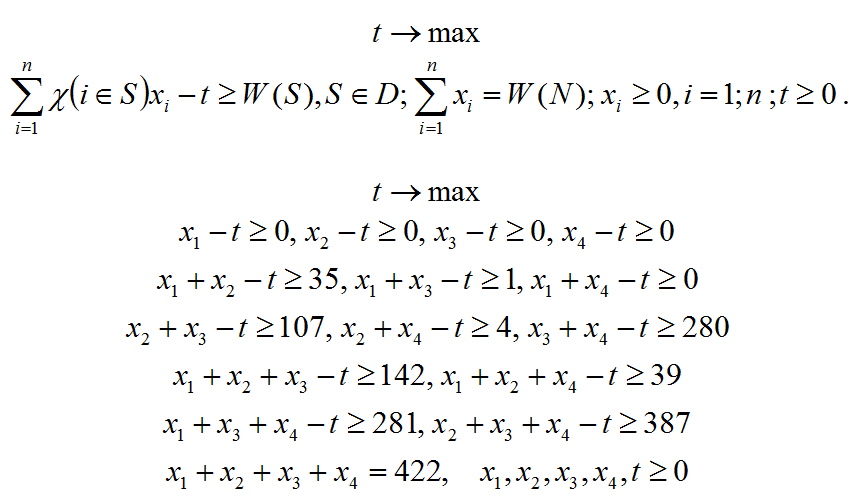

Рішення даної ЗЛП має вигляд: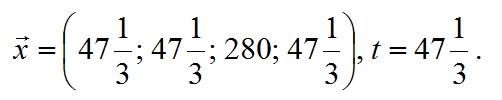

При підстановці рішення в систему неравество в рівності звертаються обмеження, відповідні коаліцій. Зауважимо, що коаліції {1}, {2} і {3,4} утворюють повну групу непересічних множин, тому заморожуємо значення, і виключаємо з системи нерівності, відповідні коаліцій і переходимо до другого етапу.

При підстановці рішення в систему неравество в рівності звертаються обмеження, відповідні коаліцій. Зауважимо, що коаліції {1}, {2} і {3,4} утворюють повну групу непересічних множин, тому заморожуємо значення 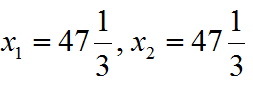, і виключаємо з системи нерівності, відповідні коаліцій і переходимо до другого етапу.

Рішення ЗЛП другого етапу має вигляд:

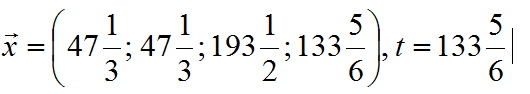
При підстановці рішення в систему нерівності, в рівності перетворюються обмеження, відповідні коаліціям . Оскільки було заморожено на попередній ітерації, то даний набір множин утворює повну групу непересічних множин на , тому заморожуємо , а оскільки значення було заморожено на попередній ітерації, то виходить, що теж фіксоване. Таким чином, всі змінні визначені і вектор на останній ітерації є n-ядром.

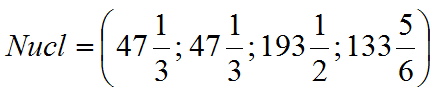
Віднімаючи з довжин радіальних маршрутів (див. (1)) компоненти n-ядра, отримуємо компоненти вектора витрат.

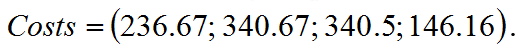
Література

1. Schmeidler D.. The nucleolus of a charecteristic function game // SIAM J on Applied Mathematics, 17, 1163-1170.
2. Grotte J.H., Computation of and observation on the nucleolus and central games // M.Sc. Thesis, Dept. of Operations Research, Cornell university.
3. Moulin H. Axioms of cooperative decision making // Cambridge university press, 1988.
4. Curiel I. Cooperative game theory and applications // Springer US, 1997.